Começa aqui nossa jornada matemática. O material aqui apresentado serve também como introdução para os capítulos referentes a Data Science e à Pesquisa de Mercado.
Utilizaremos como uma das fontes principais o livro “Modern Applied statistics with S”, de Venables e Ripley (Springer, 2002). Como o livro já é mais antigo, vamos utilizar também material mais recente. Os nossos exemplos também não serão os do livro. Vamos nos basear mais nos helps dos pacotes (packages) do software R.
É fundamental para um bom aproveitamento que estejam instalados o software R (download aqui) e o RStudio, um excelente ambiente para desenvolvimento na linguagem R (download aqui). Ambos são grátis. É interessante também utilizar uma introdução simples ao R (por exemplo, um tutorial bem básico está aqui). Existem tutoriais sobre R e RStudio no youtube.
Em todo o caso, à medida que formos apresentando os comandos, faremos um brevíssimo comentário. O material aqui apresentado será de uma forma mais leve, intuitiva mas rigorosa. Quem quiser uma apresentação mais detalhada pode acessar o próprio livro de Venables e Ripley (daqui para diante V&R).
Vamos então ao que interessa.
Simulando uma distribuição e verificando o quanto ela se desvia, por exemplo, de uma distribuição normal
Simulações serão uma de nossa principais ferramentas. Aqui vamos carregar um package (no caso o graphics); gerar uma distribuição t com 200 pontos e 5 graus de liberdade e armazenar na variável (objeto) y; plotar um gráfico qqnorm de y; plotar no mesmo gráfico uma reta (função qqline) para avaliar quão “reta” é a distribuição de y (correspondendo assim, ou não, a uma distribuição normal). Nesse caso se verifica que a distribuição t de y tem uma cauda mais longa do que uma normal.
> require(graphics) ## carregue o package ‘graphics’
>
> y <- rt(200, df = 5) ## simule uma distribuição t
> qqnorm(y) ## plote os pontos da distribuição
> qqline(y, col = 2) ## plote uma linha
>
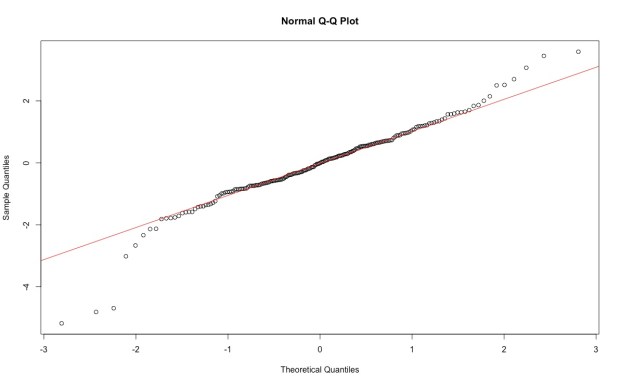
O símbolo ‘>’ indica que é um comado do R. É assim que, a partir de comandos escritos num ‘script’ , esses comandos e seus resultados são apresentados no console. Os textos abaixo indicam o que é apresentado no console.
Ajustando uma distribuição univariada: função fitdistr
Que tal ‘? fitdistr’ ?
?fitdistr
No documentation for ‘fitdistr’ in specified packages and libraries:
you could try ‘??fitdistr’
Logo ??fitdistr. Isso vai gerar uma busca não somente nos packages que já tenham sido ‘carregados’, através de um comando library(fitdistr) ou require (fitdistr). A busca é feita num ambiente mais amplo, e gera um ‘help’ que indica, entre outras informações, que a função fitdistr pertence ao package MASS. Então vamos carregar esse package. Ajustemos então uma distribuição gama e uma distribuição t:
> library(MASS) ## poderia ser também require(MASS)
> ?fitdistr ## help da função – já carregamos o package MASS
>
> ## avoid spurious accuracy
> op <- options(digits = 3) ## ‘printando’ com 3 dígitos
> set.seed(123) ## configurando a semente do gerador de números aleatórios## simulando uma ditribuição gama e armazenado em x
> x <- rgamma(100, shape = 5, rate = 0.1)## ele ajusta bem a taxa(rate) mas falha um pouquinho na forma (shape)
> fitdistr(x, “gamma”)
shape rate
6.4870 0.1365
(0.8946) (0.0196)
> ## agora com mais controle, o que não melhora muito…
> fitdistr(x, dgamma, list(shape = 1, rate = 0.1), lower = 0.001)
shape rate
6.4869 0.1365
(0.8944) (0.0196)
>
> # agora ajustando uma distribuição t
> set.seed(123)
> x2 <- rt(250, df = 9) ## t com 250 pontos e 9 graus de liberdade
> fitdistr(x2, “t”, df = 9)
m s
-0.0107 1.0441
( 0.0722) ( 0.0543)
A função fitdistr é interessante quando não conhecemos a distribuição, temos os pontos e desejamos verificar se faz sentido ajustar uma distribuição, ainda que por tentativa e êrro. Aqui não há simulação, mas uma tentaiva de identificação de média e desvio padrão. Ou outros parâmetros, como na distribuição gama acima.
Quando sabemos que ditribuição queremos simular, podemos utilizar funções como rnorm:
# configurando para gráficos em 3 ‘linhas’e 3 ‘colunas’
par(mfrow=c(3,3)) ## restaurando a configuração ‘default’: 1 ‘linha’e 1 ‘coluna’
# simulando distribuições (normal, por exemplo)
> ?rnorm# configurando a semente do gerador de números aleatórios
> set.seed(123)##300 pontos, média 0(zero) e variância 1(um) e armazenando em x
> x <- rnorm(300, mean = 0, sd = 1)## histograma de x em cor cinza, acrescentando um título
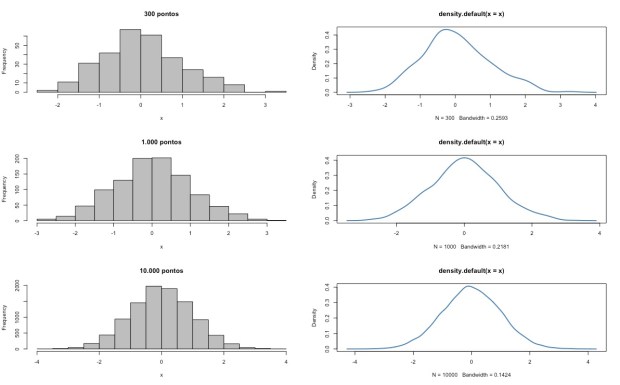
> hist(x, col=”gray”, main=”300 pontos”)
> plot(density(x), col = “steelblue”, lwd = 2) ## densidade: não muito ‘normal’…
>
> ## agora 1000 pontos
> x <- rnorm(1000, mean = 0, sd = 1)
> hist(x, col=”gray”, main=”1.000 pontos”)
> plot(density(x), col = “steelblue”, lwd = 2) ## densidade: mais ‘normal’…
>
> ## porque não 10 mil pontos?
> x <- rnorm(10000, mean = 0, sd = 1)
> hist(x, col=”gray”, main=”10.000 pontos”)
> plot(density(x), col = “steelblue”, lwd = 2) ## densidade: mais ‘normal’ ainda…
>
> # maior o número de pontos, mais próximo de uma normal
> # experimente outras funções: rbeta, rbinomial, runiform etc. (pg. 108 V&R)
>
> par(mfrow=c(1,1)) ## restaurando a configuração ‘default’: 1 ‘linha’e 1 ‘coluna’
>
Próximos posts:
- boxplots
- comparações de múltiplas amostras
- testes de hipótese
- plotando dados bi-dimensionais
e o que mais conseguirmos postar. Aguarde…
