Data Science

A introdução deste capitulo é a mesma de Análise Multivariada (ver aqui).

Mas, para iniciar vamos apresentar um livro que pode ser muito útil:

O livro é relativamente barato como e-book numa livraria virtual: cerca de US$10.

Nele você vai encontrar definições do que é NoSQL, MapReduce, Sharding e outros termos associados à area de Data Science e Big Data. É útil ter para tirar dúvidas.

Faremos agora uma rápida viagem pelo universo do Aprendizado Supervisionado (um modelo preditivo), do Aprendizado Não Supervisionado (um modelo de cluster analysis) e uma Visualização de Dados. Isso com o respectivo código / script em R, para que você possa reproduzir os exemplos.

Em seguida prosseguiremos, sempre com os respectivos scripts em R, com os passos em Data Science:

• Pré-processamento
• Aprendizado Supervisionado – modelos preditivos
• Aprendizado Não Supervisionado – cluster analysis e affinity grouping
• Aprendizado Semi-Supervisionado
• Avaliação de um modelo – precisão dos resultados (isso será apresentado em cada um dos três passos acima)
• Relacionamento com MySQL
• Visualização de Dados

Antes do Pré-processamento, vamos fazer um ‘Quick Tour’ por um modelo preditivo,  um modelo de cluster analysis e um de visualização de dados, para vermos como a coisa funciona. Se você não entender todos os detalhes não se preocupe. Ao longo da nossa trajetória tudo estará bem mais claro.

Modelos Preditivos

Vamos supor que você já criou um projeto no RStudio (um bom nome para o projeto é ‘Data Science’), baixou daqui o dataset ‘wine.csv’ e armazenou no diretório do seu projeto (talvez ‘Data Science’) esse mesmo arquivo csv. Vamos então ao R.

Lendo wine.csv, armazenando no data frame wine e dando rótulos para as colunas desse mesmo dataset wine:

> library(readr) ### para a função read_csv

### lendo o dataset e carregando no data frame ‘wine’
> wine <- read_csv(“wine.csv”, col_names = FALSE)
Parsed with column specification:
cols(
X1 = col_integer(),
X2 = col_double(),
………
X14 = col_integer()
)
>
> # dando rótulos para as colunas
> colnames(wine) <- c(“Class”, “Alcohol”, “Malic.acid”, “Ash”, “Alcalinity.of.ash” , “Magnesium”, “Total.phenols”,
+ “Flavanoids”, “Nonflavanoid.phenols”, “Proanthocyanins”, “Color.intensity”, “Hue”,
+ “OD280.OD315.of.diluted.wines”, “Proline”)

O que está acima é o que é apresentado no console. Como dito na introdução (em Análise Multivariada) o sinal de ‘>’ representa um comando. Além disso, o sinal de ‘+’  representa um outra linha, de continuação, desse mesmo comando.

O que vem agora é um tipo de pré-processamento. O modelo preditivo que utilizaremos, o randomForest, não admite dados ‘missing’. O comando is.na(wine) indica em que pontos do data frame wine existem dados missing. O R interpreta também TRUE como 1(um) e FALSE como 0(zero). A função sum verifica o resultado de is.na e soma as parcelas TRUE (isto é, 1). Como a soma é zero, não existe dado missing. A função summary (cujos resultados não são apresentados aqui, mas pode-se verificar no console quando você for processsar o script), informa, já que todos os dados são numéricos, para cada variável, os valores:

• mínimo
• primeiro quartil
• mediano
• médio
• terceiro qurtil
• máximo

> sum(is.na(wine)) ### se a soma é zero não existe ‘missing’
[1] 0
> summary(wine) ### resumo do data.frame wine

Nosso modelo irá prever a variável ‘Class’, com base nas outras variáveis do dataset. Essas outras variáveis serão aqui chamadas de ‘preditores‘. O ideal para um modelo preditivo é que os preditores sejam descorrelatados e com distribuições simétricas cada um. Não vamos examinar agora as distribuições. Faremos no futuro. Mas vamos examinar as correlações, sob a forma gráfica:

> library(corrplot)

### plotando a correlação entre as variáveis com exceção de “Class’ (coluna 1)
> corrplot(cor(wine[ , -1]))

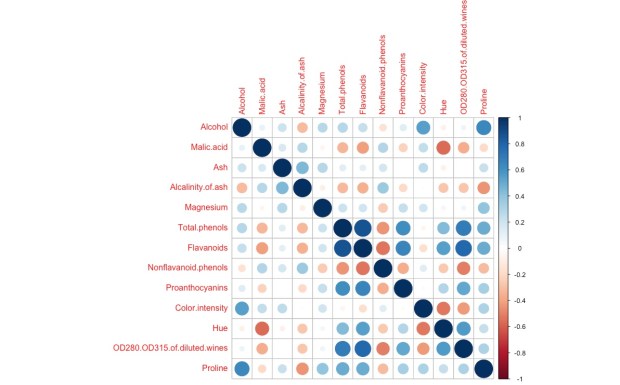
Quanto mais azul, a correlação é mais próxima de +1.  Quanto mais vermelho, de -1. Nota-se que, de uma maneira geral, os preditores são descorrelatados. Na prática, jamais teremos uma coisa perfeita.

Vamos agora transformar a variável numérica Class numa variável do tipo fator.  Em seguida vamos dividir o data set num data frame de treinamento e um de teste. A fração com que vamos dividir é 70% para teinamento e o resto para teste:

wine$Class <- factor(wine$Class) ### transformando Class de numérica para fator
>
> frac <- 0.7 ## fração para treinamento (70%) e teste (30%)

## seleção aleatória das linhas do data.frame wine
> indtrain <- sample.int(nrow(wine), frac * nrow(wine))

## nrow(wine) é o número de observações de wine

## seleção para treinamento e teste
> train <- wine[ indtrain, ] ## data.frame para treinamento
> test <- wine[-indtrain, ]  ## data.frame para teste
>

Vamos utilizar como modelo preditivo, como dissemos acima, o randomForest. É um dos modelos que prefiro. É flexível e tem, via de regra, um bom ou excelente desempenho.

Vamos carregar o package,  treinar o modelo (armazenando o resultado / objeto em mod.rf) , plotar um gráfico com as importâncias de cada variável no modelo preditivo, efetuar uma predição, armazenando essa predição em pred.wine e tabulando a predições contra os valores reais que já tínhamos no dataset de treinamento. Como vemos, quase todos os pontos se encontram na diagonal: o previsto é igual ao real. Só duas observações foram previstas incorretamente.

> library(randomForest)
> mod.rf <- randomForest(factor(Class) ~., data=train, importance=TRUE) ## treinando o modelo
> varImpPlot(mod.rf) ## importância das variáveis no modelo
>
> pred.wine <- predict(mod.rf, newdata=test) ## prevendo o data.frame de teste
> (conf.mat <- table(test$Class, pred.wine)) ## tabulação cruzada
pred.wine
1 2 3
1 19 0 0
2 0 20 2
3 0 0 13
>

Agora o gráfico com as importâncias. Verifica-se que, nos dois critérios de importância, Color.intensity, Flavanoids e Proline são os preditores mais importantes. Ash e Nonflavanoid.phenols são os de menor importância. Muitas vezes, o que, como veremos, não é o caso aqui, é necessário utilizar uma ‘navalha de ockam’, retirando do modelo variáveis menos importantes que, podem, possivelmente, ser mais ruído do que informação.

 

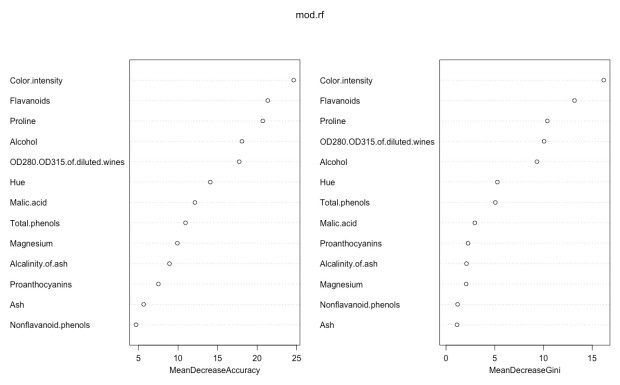
Finalmente, vamos verificar a precisão das estimativas, com coeficientes adequados. Para isso, vamos utilizar a função classAgreement, do package e1071. O coeficiente diag também é chamado de hit-rate. O modelo acertou em 96,3% dois casos. O coeficiente kappa é um ‘hit-rate’ que desconta o fato de que alguns  grupos sejam bem maiores do que os outros, e, eventualmente, inflar o hit-rate. Normalmamte kappa é menor que diag, e  aqui ele tem valor alto (0,94 – 94%): os grupos tem tamanho 19, 20 e 15. Os coeficientes rand e crand são mais utilizados para Aprendizado Não Supervisionado (no caso de cluster analysis – ver abaixo).

>
> library(e1071)
> classAgreement(conf.mat, match.names=TRUE ) ## verificando a precisão
$diag
[1] 0.962963

$kappa
[1] 0.94375

$rand
[1] 0.9538784

$crand
[1] 0.8957971

 

Cluster Analysis

Vamos agora ao Aprendizado Não Supervisionado, exemplificando com Cluster Analysis. Inicialmente vamos simular, com o package clusterGeneration, 5 grupos / clusters, com um grau de separação  sepVal=0.3, isto é, bem separados, com duas variáveis (numNonNoisy=2) e 5 outliers. Vamos criar dois datasets, mas só vamos utilizar um deles: tmp1$datList$chk1_1. Os dados serão armazenados num dataframe data. O comando head(data) apresenta as seis primeiras observações de data (se quisermos 10 basta adicionar o parâmetro n=10). Iremos também armazenar as informações dos clusters / grupos originais no vetor clusters.

> library(clusterGeneration)
>
> tmp1 <- genRandomClust(numClust=4, sepVal=0.3, numNonNoisy=2,
+ numNoisy=0, numOutlier=5, numReplicate=2, fileName=”chk1″) ## gerando o dataset
>
> data <- tmp1$datList$chk1_1 ## armazenando em ‘data’
> head(data)
x1                x2
[1,] 23.886651 0.9085447
[2,] 33.086564 2.6109816
[3,] 29.548261 -5.6006288
[4,] -1.274899 10.2997713
[5,] 17.880857 0.8297561
[6,] 7.704335 -2.9219771
>
> clusters <- tmp1$memList$chk1_1 ## armazenado o vetor com os clusters originais

Em seguida vamos efetuar a ‘clusterização’ / agrupamento com a função pam do package cluster, e armazenar o vetor que indica os cluster formados no agrupamento clusters no vetor clustering. Fazemos a tabulação cruzada dos valores originais e dos provenientes do agrupamento. Colocando o comando entre parêntesis faz com que os resultados sejam ‘impressos’ no console. O grupo 0(zero) original corresponde aos outliers. Esses outliers foram agrupados na clusterização. Os coeficientes diag e kappa aqui não fazem sentido, mas rand e crand sim: são valores altos, até porque os grupos são bem separados. Veja o gráfico abaixo.

 

>
> library(cluster)
> clustering <- pam(data, 4)$clustering        ## efetuando a cluster analysis
> (conf.mat <- table(clusters, clustering))     ## tabulação cruzada
clustering
clusters 1 2 3 4
0 3 0 1    1
1 0 0 2 179
2 0 0 157 0
3 0 173 0 0
4 179 0 0 0
>
> library(e1071)
> classAgreement(conf.mat, match.names=TRUE ) ## verificando a precisão dos resultados
$diag
[1] 0

$kappa
[1] -0.3305667

$rand
[1] 0.9935563

$crand
[1] 0.9827164

Pelosvalores de rand(0.99) e crand(0.98) verificamos que a função pam foi capaz de reproduzir  quase todo o agrupamento origina (cerca de 98 a 99%).

Plotando agora o gráfico do agrupamento final. Para identificar os grupos, vamos associá-los a cores:

> ### definido cores para a plotagem
> col.clust <- rep(“black”, length(clustering))
> for ( i in 1:length(clustering)) {
+ if (clustering[i] == 1) col.clust[i] <- “red”
+ if (clustering[i] == 2) col.clust[i] <- “darkgreen”
+ if (clustering[i] == 3) col.clust[i] <- “steelblue”
+ if (clustering[i] == 4) col.clust[i] <- “darkorange”
+ }
>
> plot(data, col= col.clust, ylim= c(-50, 40))

## plotando os clusters nas variáveis x1 e x2
>

 

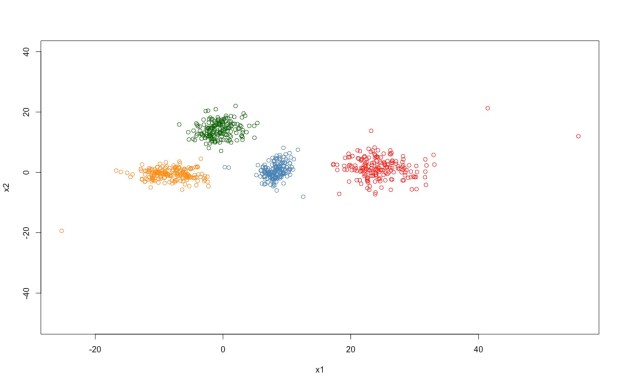
Data Visualization

Finalmente, vamos dar uma idéia do que é Visualização de Dados. Gosto muito de iniciar esse tema com um dataset  do Titanic, que informa, entre outras variáveis, os sobreviventes daquela tragédia por Classe, Sexo e Idade.

Em tempo: não se decora sintaxe de uma linguagem. Com o uso, ao longo do tempo, a coisa vai sendo fixada. Em qualquer situação sempre é possível digitar ?qualquercoisa ou ??qualquercoisa.

Agora faça o download do arquivo em Excel (xls) aqui . Armazene no diretório do seu projeto do RStudio. Agora vamos ler o arquivo e armazenar em titanic. Vamos visualizar o dataset (isso não é apresentado aqui mas você verá quando processar)  e as 8 primeiras observações:

library(readxl)
> titanic3 <- read_excel(“titanic3.xls”)

Warning message:
In read_fun(path = path, sheet = sheet, limits = limits, shim = shim, :
Coercing text to numeric in M1306 / R1306C13: ‘328’
> View(titanic3)    ### Não apresentado no site
> head(titanic3, n=8)

Verificando agora as dimensões de titanic3  (1309 observações e 14 variáveis) e a sua estrutura

> dim(titanic3)
[1] 1309 14

> str(titanic3)
Classes ‘tbl_df’, ‘tbl’ and ‘data.frame’: 1309 obs. of 14 variables:
$ pclass : num 1 1 1 1 1 1 1 1 1 1 …
$ survived : num 1 1 0 0 0 1 1 0 1 0 …
$ name : chr “Allen, Miss. Elisabeth Walton” “Allison, Master. Hudson Trevor” “Allison, Miss. Helen Loraine” “Allison, Mr. Hudson Joshua Creighton” …
$ sex : chr “female” “male” “female” “male” …
$ age : num 29 0.917 2 30 25

………………

Vamos modificar o data set para tornar mais conveniente a visualização. Inicialmente definiremos a variável agegroup. Essa variável será um fator, com elementos do tipo cadeia de caracteres (“child” ou “adult”). Faremos a codificação com a função vetorial ifelse (ver ?ifelse).

> # recodificando a idade para agegroup (criança se menor do que 10 anos)
> agegroup <- “adult”
> agegroup <- ifelse(titanic3$age < 10, “child”, agegroup)
> # poucas crianças
> table(agegroup)
agegroup
adult child
964    82

Idem para class e survived:

> class <- “3rd”
> class <- ifelse (titanic3$pclass == 2, “2nd”, class)
> class <- ifelse (titanic3$pclass == 1, “1st”, class)
> table(class)
class
1st 2nd 3rd
323 277 709
> # codificando a variável survived
> survived <- “no”
> survived <- ifelse (titanic3$survived == 1, “yes”, survived)
> table(survived)
survived
no yes
809 500

Agora juntando em colunas (cbind junta as colunas numa matriz) as quatro variáveis que iremos plotar.  Daremos rótulos para as colunas da matriz e apresentaremos as seis primeiras linhas da matriz titanic.

## matriz ‘titanic’
> titanic <- cbind(class, titanic3$sex, agegroup, survived)
> is.matrix(titanic)
[1] TRUE
> # rotulando as colunas
> colnames (titanic) <- c(“class”, “sex”, “agegroup”, “survived”)
> head(titanic)
class sex agegroup survived
[1,] “1st” “female” “adult” “yes”
[2,] “1st” “male” “child” “yes”
[3,] “1st” “female” “child” “no”
[4,] “1st” “male” “adult” “no”
[5,] “1st” “female” “adult” “no”
[6,] “1st” “male” “adult” “yes”
>

e, finalmente, plotamos um parallel coordinate plot:

> require(extracat)
> scpcp(data=titanic,sel=”survived==’yes'”, sel.palette = “d”)

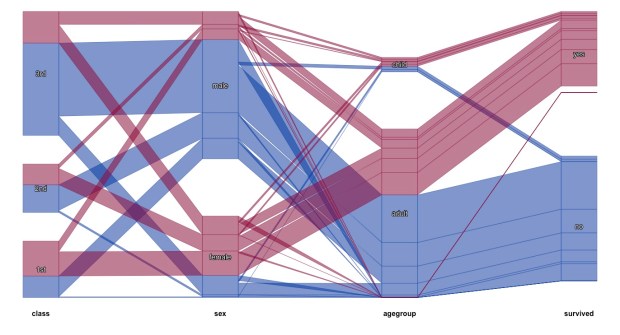
Todos os dados de titanic (as 1309 linhas)  são plotadas.  Selecionamos para identificação a coluna survived (sel=”survived==’yes’). Escolhemos a palette=”d” (ver ?getcolors do package extracat).

É possível ver, por exemplo, que:

• mais de metade das mulheres sobreviveu
• bem mais da metade daqueles da terceira classe não sobreviveu
• pouco mais da metade da primeira classe sobreviveu
• quase não havia crianças a bordo e pouco mais da metade sobreviveu
• no conjunto, quase o total do percentual de sobrevivência foi de mulheres adultas, em todas as classes.